海豹桌遊123：《數感傳奇》三部曲（二）

《數感傳奇》三部曲．限量優惠單

老實說這次綿羊犬出了個大難題給我。

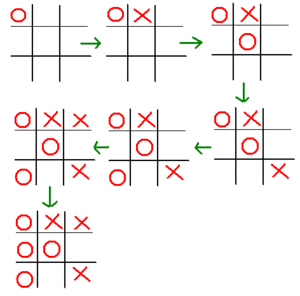
這次為了要能夠呈現一個遊戲的數學原理，遊戲必須簡單到可以用數學去分析一個優勢路徑。但就遊戲設計理論而言，你的第一課就是要避免優勢路徑的存在，不然只要玩家發現必勝法後，這個遊戲就崩潰了。

簡單的來說，我被夾在分析容易跟分析困難之間。要讓我們能夠簡單的呈現一款遊戲背後的數學原理，這個遊戲必須能夠被簡單的分析。但要讓遊戲富有遊戲性與思考空間，分析就又同時必須夠困難。

解決方法？提供基本版與完整版，其中基本版會存在優勢策略，然後加進新的機制把優勢策略消滅掉。

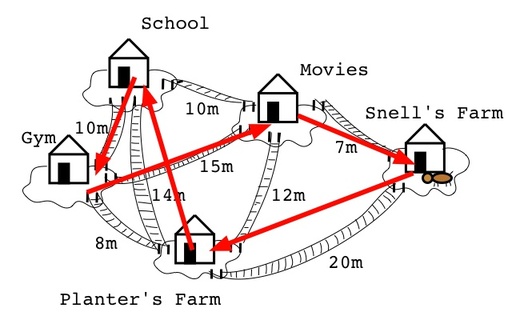
我以圖論的問題為例。在圖論遊戲中，我們討論的其實是有名的推銷員問題：給定若干個城市以及之間的移動成本，如何尋找一個成本最小的路徑來拜訪所有城市？求這個最小路徑是個困難的演算法問題，但無論如何，它必然存在一條路徑，而只要找出這條路徑，遊戲就崩潰了。

解決方法？在進階版，我們讓這些成本是隨機的，而且會隨著遊戲過程而變動。如此一來，遊戲的分析就變的困難，你不再能在遊戲準備時就看出一條最佳路徑，然後躺著玩完遊戲，因為這個最佳路徑隨時都在調整。

我們在另外兩款遊戲中也做了類似的處理，運用數學工具製造一個可分析的基本版，然後利用遊戲設計的機制論，在完整版讓決策分析變得困難。希望這樣的處理，可以同時帶給大家數學與遊戲的雙向樂趣。

保重 - A劇團 < 尋找三藏 >

A劇團今年藝穗節的新製作＜尋找三藏＞第一周演出剛結束，很開心竹馬組的編曲＜保重＞獲得不少好評。在這邊我要來澄清一下，並趁機分享一些我編作曲上的理念。

因為這首歌在某種程度上來說，不算是我寫的。這首歌的credit，是作詞蕭文華的。

一個極盡瘋狂的實驗 - A劇團 < 尋找三藏 >

活動頁面／購票連結

去年藝穗節Ａ劇團搞了密室逃脫音樂劇。沒想到今年，我們又幹了更瘋狂的事情...

我們一直試圖在尋找阿卡貝拉音樂劇的可能性，從最開始2011年藝穗節的＜尋找不理門＞，到去年戲劇中的戲劇，密室逃脫＜彼得潘遊戲＞；到結合各地兒歌，給孩子們的＜阿卡的兒歌大冒險＞；乃至於到跟思劇場合作的，有沒有搞錯居然還玩傳統戲曲的＜Ace計畫＞。還有什麼？

這次，我們從設計群下手。我們跨出原有的不點＋海豹組合，跟新的編劇、新的導演、新的音樂合作。

更精確地說，我們幹了以下這幾件事情：

1. 首先，由四個編劇各寫一個小劇本。
2. 接著有兩個劇組，每個劇組有不同的導演跟演員。每個劇組會被分配到其中三份劇本，也就是說，有兩個劇本會在兩個劇組都演，會被以完全不同的方式呈現。
3. 如果嫌這還不夠的話，兩個劇組的音樂設計也是不一樣的：不點導的那組是由不讀書俱樂部的芯慈作曲，而我作曲的那組由Be劇團的彥霆導演。

結果就是我們要一次面對新的編劇、新的導演、新的音樂設計，搞到自己快吐血...

但是是值得的。

在第一次兩劇組會面順走後，我非常慶幸我們當初做了這個決定。這次的雙劇組製作，我們看見了很多阿卡音樂劇的可能性，不論就編劇、就導演、就音樂乃至於就演員上，不同的呈現方式，不同的批判，不同的觀照。

希望大家一起來看看，這些新的可能性。拜託大家要來，不然有人會生氣：

購票連結 ▶ http://goo.gl/0bXqoS
劇情介紹 ▶ https://goo.gl/HDbWBS

➢ 演出時間：每場 60 分鐘
8/18-19　19:00 青梅 ❀、20:30 竹馬 ♘
8/24-26　19:00 竹馬 ♘、20:30 青梅 ❀
　
➢ 票　　價：每場 300 元
➠蒐集全套西遊　可享 2張500元 優惠
➠四人同行取經　可享 每張85折 優惠

海豹桌遊123：《數感傳奇》三部曲（一）

《數感傳奇》三部曲．限量優惠單

日前綿羊犬已經公布了這個消息：海豹這次和綿羊犬以及賴以威教授的數感實驗室合作，推出這一系列的數感遊戲。

身為一個以數學奧林匹亞、統計研究為背景的桌遊人，我還滿常被問說：＂有沒有推薦的數學遊戲？＂而當我拿出一款遊戲時，對方困惑的看著我說：＂這沒有加減乘除啊，數學在哪裡？＂

這句話每次都會讓我有滿深的感觸，那就是：

我們對數學的想像太狹隘了！！

或許是因為我們教育體制的關係，我們的數學＂課＂經常環繞著加減乘除、解方程式、三角函數等等，以至於我們常常會認為那些xyz，平方開根號就是數學。

不對，那是數學符號，不是數學。數學是一種解決問題的方法，而不是表面的呈現方式。這就像文字跟文學是不一樣的。

這一點其實在桌遊設計裡非常明確。身為一個桌遊設計師，我經常被要求從數學的角度去解決一些沒有數字、沒有算式的問題。

最常見的：這個遊戲有沒有必勝法？

這其實是個非常數學的問題：你試圖在無窮無盡的遊戲方法中，試圖去推理出有沒有某一個人會有必勝或是近乎必勝的策略。你必須去分析這款遊戲，排除沒有希望的策略，再進一步去分析。

這個過程其實大家都做過。舉例來說，圈圈叉叉：

就算沒有經過任何＂數學課＂訓練的人，也可以慢慢推理出圈圈叉叉是個必和的遊戲。事實上，根本有個大定理告訴你，如果一個無隨機性的遊戲有回合上限（圈圈叉叉是九回合），則要不有一方必勝，不然就是必和。

於是就有遊戲設計師去思考：那有沒有辦法讓圈圈叉叉不必勝？

然後他就意識到，唯一的方法就是讓這個遊戲沒有回合上限。

於是就出現了＜奇雞連連＞這款遊戲：

這上面其實都是很數學的思考過程：我要尋找一個答案（非必和的圈圈叉叉），而為了求這個答案，我先去分析既有的結果（有限回合必和），從而得到我想要的解答。這跟我知道x+y>2，x<1，因此y>1，思考上並沒有甚麼不同。

只是沒有符號而已。數學，它一直都在，以各種不同的形式，出現在不同的地方，不論是課堂、遊戲，乃至於真實人生。

我們希望透過這一系列的遊戲，不論是從遊戲設計或是從主題包裝上，可以讓孩子們卸去對數學表層的恐懼，去更深刻的理解到，原來數學是這麼一回事！

希望這個系列，能夠忠實地傳遞，這樣的想法。