身為一個以數學奧林匹亞、統計研究為背景的桌遊人,我還滿常被問說:"有沒有推薦的數學遊戲?"而當我拿出一款遊戲時,對方困惑的看著我說:"這沒有加減乘除啊,數學在哪裡?"
這句話每次都會讓我有滿深的感觸,那就是:
我們對數學的想像太狹隘了!!
或許是因為我們教育體制的關係,我們的數學"課"經常環繞著加減乘除、解方程式、三角函數等等,以至於我們常常會認為那些xyz,平方開根號就是數學。
不對,那是數學符號,不是數學。數學是一種解決問題的方法,而不是表面的呈現方式。這就像文字跟文學是不一樣的。
這一點其實在桌遊設計裡非常明確。身為一個桌遊設計師,我經常被要求從數學的角度去解決一些沒有數字、沒有算式的問題。
最常見的:這個遊戲有沒有必勝法?
這其實是個非常數學的問題:你試圖在無窮無盡的遊戲方法中,試圖去推理出有沒有某一個人會有必勝或是近乎必勝的策略。你必須去分析這款遊戲,排除沒有希望的策略,再進一步去分析。
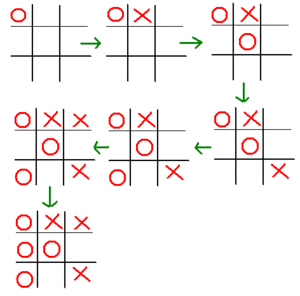
這個過程其實大家都做過。舉例來說,圈圈叉叉:
就算沒有經過任何"數學課"訓練的人,也可以慢慢推理出圈圈叉叉是個必和的遊戲。事實上,根本有個大定理告訴你,如果一個無隨機性的遊戲有回合上限(圈圈叉叉是九回合),則要不有一方必勝,不然就是必和。
於是就有遊戲設計師去思考:那有沒有辦法讓圈圈叉叉不必勝?
然後他就意識到,唯一的方法就是讓這個遊戲沒有回合上限。
於是就出現了<奇雞連連>這款遊戲:
這上面其實都是很數學的思考過程:我要尋找一個答案(非必和的圈圈叉叉),而為了求這個答案,我先去分析既有的結果(有限回合必和),從而得到我想要的解答。這跟我知道x+y>2,x<1,因此y>1,思考上並沒有甚麼不同。
只是沒有符號而已。數學,它一直都在,以各種不同的形式,出現在不同的地方,不論是課堂、遊戲,乃至於真實人生。
我們希望透過這一系列的遊戲,不論是從遊戲設計或是從主題包裝上,可以讓孩子們卸去對數學表層的恐懼,去更深刻的理解到,原來數學是這麼一回事!
希望這個系列,能夠忠實地傳遞,這樣的想法。


沒有留言:
張貼留言